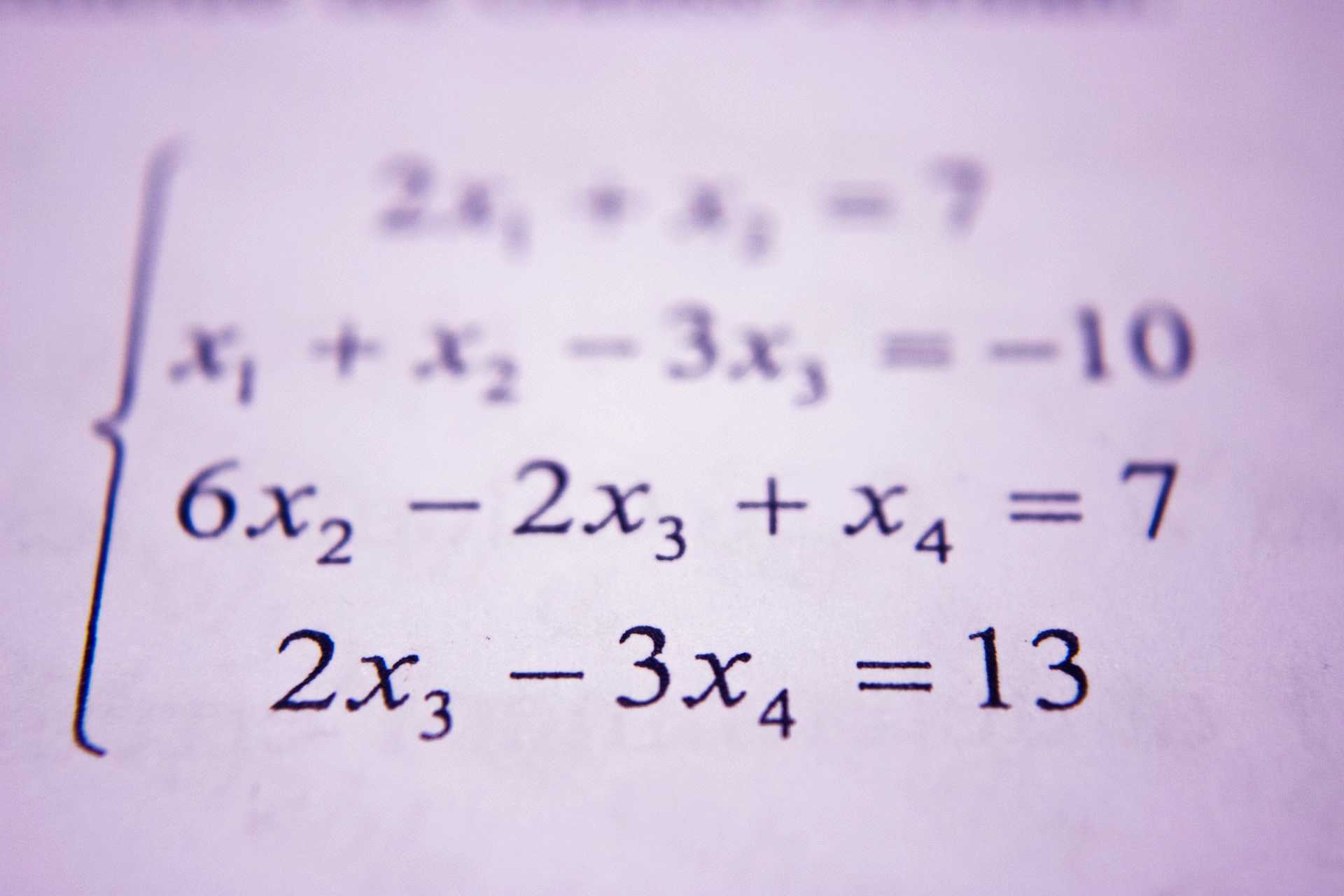Matrices are arranged as vertical and horizontal lines and the entrances are made in columns and rows by the method of expressions, symbols, and an array of figures that is rectangular, and these distinct items are termed as entries or elements. The common method of the script of the matrices is in box brackets. The rows and columns that a matrix has, describes its size. A Matrix that has n columns and m rows is termed m × n matrix, while the letters m and n are called dimensions.
Matrix has a long past for resolving linear equations through applications. It was previously labeled as arrays. James Sylvester, in 1850 named it the Matrix. As per him, the matrix was like an object that provided rise to a lot of features called minors, which means elements of matrices that emerge from the one that is unique by eradicating rows and columns. Cullies, an English mathematician then, was the foremost who made use of bracket notation in 1913, that year. Matrices are used to proficiently work and write employing multiple equations, which is referred to as the arrangement of linear equations, concurrently.
If the magnitude of the matrices is similar (having the same sum of columns and rows), addition and subtraction can be done entry by entry. There is a precise rule for the multiplication of matrices that says that two matrices can only be multiplied if the count of columns and the count of rows in the first and the second are equal. So, each and every matrix multiplication can be carried out entry-wise in the associated field with a scalar.
Different Kinds of Matrices:
1. Row Vectors: Contain a single row.
2. Column Vectors: Contain a single column.
3. Square Matrix: The count of rows and numbers is similar to this one.
4. Empty Matrix: This kind of matrix does not have rows and columns and is generally used in algebra programming in computers.
Numerous operations are useful to alter matrices, scalar multiplication, addition, and subtraction. Matrices work with all these basic techniques.
These methods are further used to calculate amounts, differences, and information of products such as beverages of various flavors: Guava, Aloe vera, and litchi having separate packaging: bottles or cartons. Different techniques of Matrix are used to calculate figures like monthly and yearly sales, sales as per each flavor, each packaging, and so on.
Scalar Multiplication, Addition, and Subtraction
Matrices are used for representing systems and listing data. The operation on matrices is performed because the entries are made with numbers. The addition or subtraction can only be done if the dimension of the matrices is the same. Addition in the Matrix is commutative and associative.
The properties of Scalar Multiplication
- Right and left distributivity
- Additive inverse
- Null
- Identity
- Associativity
Matrices have various applications but the major one is the representation of linear transformations (it means generalizing the linear functions, like f(x) = 5x). Let us understand with the help of this example, vectors rotation in a space that is three-dimensional is a linear transformation, the representation of which can be R rotation matrix: if the column vector is considered as V (a matrix that just has one column) that describes the position in that space of that point, the final product Rv is the vector that describes the position after rotation. The final product of two transformation matrices is a matrix that denotes the composition of two transformations. Additional application of matrices is the result of the systems of linear equations.
As discussed above, these are the concepts of Matrices that can further help you in understanding the subject better. Any subject of mathematics requires a lot of practice, you can find several explanations on the internet these days, best tips and tricks are provided by Cuemath, they provide easy-to-understand solutions for tricky matrix multiplication as well. So, here’s wishing you all the best for preparing and mastering the concepts of Matrices.